|
|
The report "Radiocarbon dating the Turin Shroud", Damon et al, in Nature, (Vol.337, Nr. 6200 pages 611-615. 16 Feb. 1989) concludes:
| Table 1 (Only for the Shroud) | d13C | Table 2 |
| Ar. 591-+30 690-+35 606-+41 701-+33 | -25 | 646-+31 689-+16* |
| Ox. 795-+65 730-+45 745-+55 | -27 | 750-+30 691-+31' |
| Zu. 733-+61 722-+56 635-+57 639-+45 679-+51 | -25.1 | 676-+24 |
| * = Weighted mean ' = Unweighted mean. | X2 = 6.4 | |
| %SL. = 5 |
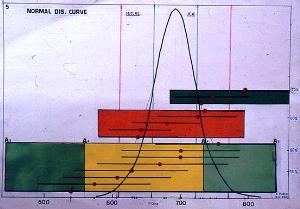
The reason for a statistical analysis of radiocarbon dates, is the FACT that, theoretically, no experimental result is absolute, and to some extent, subject to chance error. Even an EXACT measurement is still due, to some extent, to chance. Statistical analysis enables the analyst, to determine, with a pre-determined degree of confidence, (here claimed to be at least 95% ) the degree of variations which are due to chance and to known and unknown influences. When applying statistical tests, caution should be observed with data suspected of appreciably differing from a normal distribution.
Examples of distributions:
Normal = Z. Student = t. Chi^2 = X^2. Inverted Beta
= F.
The British Museum, selected the Chi^2 to be the criterion for the assessment
of the radiocarbon dating results for the Shroud. The MAXIMUM Chi^2 test
value for 95% confidence and (3-1) degrees of freedom is 5.99. Theoretically,
if the calculated Chi^2 test value could have occurred only by chance,
with a probability LESS than that selected, then the set of data
would be considered as being DIFFERENT. In practice : Any Chi^2
test value LARGER than 5.99, excludes the claimed 95 % confidence.
|
|
|
First I reworked the data given in Tables 1 & 2, using the classical
statistical analyzing method, based on the "Central Limit Theorem." I used
the method given in "Perry's Chemical Engineer's Handbook", my technical
bible for many years. Note that I only verify the assessment of the radiocarbon
dating results, NOT the conversion into calendar ages. All calculations
are made on a Sharp PC 4700, using an Ability (Lotus) Spreadsheet. None
of the results presented here are biased. Due to rounding up numbers, small
differences may occur. For non-mathematical minds, all calculations are
worked out completely. The use of complicated formulas is limited to the minimum.
|
Table 1 Means
|
Table 2
|
| Ar. (591+690+606+701)/4 = 647 | F-test = 4.7 > 4.26 = Reject. |
| Ox. (795+730+745)/3 = 757 | (647+757+682)/3 = 695 (Un.Mean) |
| Zu. (733+722+639+635+679)/5= 682 | (2588+2270+3408)/12 = 689 (W.Mean) |
| Ar. | {[(591-647)^2+...........+(701-647)^2]/(3x4)}^0.5 = 28 |
| Ox. | {[(795-757)^2+(730-757)^2+(745-757)^2]/(2x3)}^0.5 = 20 |
| Zu. | {[(733-682)^2+...........+(679-682)^2]/(4x5)}^0.5 = 20 |
| UM. | {[(647-695)^2+(757-695)^2+(682-695)^2]/(2x3)}^0.5 = 32 |
| WM. | {[(647-689)^2+(757-689)^2+(682-689)^2]/(2x3)}^0.5 = 33 |
| Arizona | Oxford | Zurich | U.Mean | W.Mean | |
| Nature | 646-+31 | 750-+30 | 676-+24 | 691-+31 | 689-+16 |
| Computer | 647-+28 | 757-+20 | 682-+20 | 695-+32 | 689-+33 |
Because the errors based on the scatter are NOT quoted errors, I did not use the X^2 test, but the more powerful F-test, based on the combination of the 3 means and 12 independent measurements. For 95% confidence, and (3-1) - (12-3) degrees of freedom the maximum F-test, value is 4.26. By chance alone, F should be -+ 1.
Ari |
Oxf |
Zur |
||
701 |
795 |
733 |
||
690 |
745 |
722 |
||
606 |
730 |
679 |
||
591 |
639 |
|||
635 |
||||
Sums |
2588 |
2270 |
3408 |
= 8266 |
/4 |
/3 |
/5 |
/12 |
|
Mean |
647 |
757 |
682 |
689 |
Between laboratories
=2588^2/4+2270^2/3+3408^2/5-8266^2/12=21066
Residual = (701-647)^2+.............(635-682)^2=20167
Total = Sum (Between laboratories + Residual) =41233
| Source of Variation | Sum of Squares | Degrees of Freedom | Mean Square | F Ratio < 4.26 |
| Between |
21066
|
3-1
|
21066/2=10533 | 10533/2241 = 4.7 |
| Residual |
20167
|
12-3
|
20167/9= 2241 | Conclusion : |
| Total |
41233
|
11
|
4.7 > 4.26 |
Conclusion :
An F-test value of 4.7 > 4.26, states there is a SIGNIFICANT DIFFERENCE
between the results given by the three laboratories. In regard to the tabulated
data, given in Table 1 of Nature, a certain amount of unexplained
variation of the individual runs within and between laboratories is indicated.
Student t distribution test.
The t test compares the sub mean -+error to the final mean. AMS date
for 1 run are the mean of about 10 measurements and assuming that the quoted
error is equal to the standard error, given in Nature. Because we
have to deal with a two tail test, we have to take the critical t value
2.26 for 97.5% confidence and (10-1) degrees of freedom.
|
Arizona : 646-+28
|
Oxford : 757-+20
|
Zurich : 682-+20
|
| (701-646)/33 = 1.67 | (795-757)/65 = 0.58 | (733-682)/61 = 0.84 |
| (690-646)/35 = 1.26 | (757-745)/55 = 0.22 | (722-682)/56 = 0.71 |
| (646-606)/41 = 0.98 | (757-730)/45 = 0.60 | (682-679)/51 = 0.06 |
| (646-591)/30 = 1.83 | (682-639)/45 = 0.96 | |
| (682-635)/57 = 0.82 |
|
Arizona
|
Oxford
|
Zurich
|
| (701-689)/33 = 0.36 | (795-689)/65 = 1.63 | (733-689)/61 = 0.70 |
| (690-689)/35 = 0.03 | (745-689)/55 = 1.02 | (722-689)/56 = 0.59 |
| (689-606)/41 = 2.02 | (730-689)/45 = 0.91 | (689-679)/51 = 0.20 |
| (689-591)/30 = 3.27 | (689-639)/45 = 1.11 | |
| (689-635)/57 = 0.95 | ||
This test indicates that the Arizona date 591-+30 is probably an OUTLIER. Later I tested the individual dates also by a NEW developed test, called the IEM-EEM criterion (Scott et al. 1990). Here the QUOTIENT of the difference between measurement and final mean is divided by the square root of the sum of BOTH the squared errors, it should be < 1.
|
IEM = < 1
|
EEM = < 1
|
|
Arizona 646-+17
|
Mean = 672-+13
|
| (701-646)/(17^2+33^2)^0.5 = 1.49 | |
| (690-646)/(17^2+35^2)^0.5 = 1.13 | (672-646)/(17^2+13^2)^0.5 = 1.21 |
| (646-606)/(17^2+41^2)^0.5 = 0.91 | |
| (646-591)/(17^2+30^2)^0.5 = 1.59 | |
|
Oxford 749-+31
|
|
| (795-749)/(30^2+65^2)^0.5 = 0.64 | |
| (749-745)/(30^2+55^2)^0.5 = 0.06 | (749-672)/(30^2+13^2)^0.5 = 2.35 |
| (749-730)/(30^2+45^2)^0.5 = 0.41 | |
|
Zurich 676-+24
|
|
| (733-676)/(24^2+61^2)^0.5 = 0.87 | |
| (722-676)/(24^2+56^2)^0.5 = 0.75 | |
| (679-676)/(24^2+51^2)^0.5 = 0.05 | (676-672)/(24^2+13^2)^0.5 = 0.15 |
| (676-639)/(24^2+45^2)^0.5 = 0.73 | |
| (676-635)/(24^2+57^2)^0.5 = 0.66 |
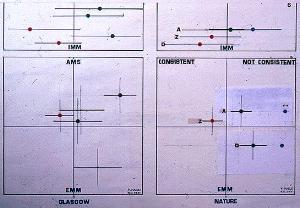
Following the criterion, proposed by Dr. Scott et al, the dates for
Arizona (3 x IEM + EEM ) and Oxford (EEM), are OUT of range. Upon
meeting Dr. Scott at a Shroud Symposium in New York, I asked her in writing,
to verify the Nature dates by the IEM-EEM criterion. But Dr. Scott
refused a direct answer.......promising the reply by letter. I am still
waiting.
|
|
I asked the British Museum for some explications. Dr. Morven Leese explained
the LOW Arizona errors as follows : Arizona did not send in FOUR,
but EIGHT "paired" dates, each pair measured the same day, with
the same set of standards and blanks. The EIGHT "dependent" dates
were combined in FOUR "independent dates, given in Table 1 (Nature).
Each pair of DEPENDENT dates are combined into an INDEPENDENT
date.
| A: 606-+41 574-+45 >>>> [606/41^2 + 574/45^2]/[1/41^2 + 1/45^2] = 591 |
|
Error = [1/(1/41^2 + 1/45^2)]^0.5 = 30
|
| B: 753-+51 632-+49 >>>> [753/51^2 + 632/49^2]/[1/51^2 + 1/49^2] = 690 |
|
Error = [1/(1/49^2 + 1/51^2)]^0.5 = 35
|
|
C: 540-+57 676-+59 >>>> [540/57^2 + 676/59^2]/[1/57^2 + 1/59^2]
= 606
|
|
Error = [1/(1/57^2 + 1/59^2)]^0.5 = 41
|
| D: 701-+47 701-+49 >>>> [701/47^2 + 701/47^2]/[1/47^2 + 1/47^2] = 701 |
|
Error = [1/(1/47^2 + 1/47^2)]^0.5 = 33
|
Yet mathematically correct, this "re-calculation" should have been notified
by the authors of the report. At first, the "combination" was silently
denied. It took more than TWO years before Arizona confirmed the
combination made at the request of the British Museum. The arbitrary "enlarging"
of the error from 17 to 31 was never solved. The best results were obtained
by averaging the paired errors.
[41 + 45]/2=43 [51 + 49]/2=50 [57 + 59]/2=58 [47 + 47]/2=47
Error on the mean : [1/(1/43^2 + 1/50^2 + 1/58^2 + 1/47^2)]^0.5 = 24.
Based on the scatter, the standard error is 28. At first, I believed
that the error was due to the fact, that Arizona included the error in
delta 13C at a later stage. The D13C error can be estimated : 31 = [28^2
+ (D13C)^2]^0.5
D13C = [961 - 784]^0.5 = 13.
The value appears to be too large. The British Museum gave several
versions, but no specific answer was given........Dr. Leese explained also that the British Museum did not use the classical method, but a NEW method, developed by the Australian scientists
Drs. Wilson & Ward. (Archeometry 20. 1978). I am still grateful to
Drs. Wilson & Ward for their precious help. The method is based on
the QUOTED error for each measurement. Quoted errors do incorporate
the statistical (counting) error, the error of the scatter of results for
standard and blanks, and the (small) uncertainty in the delta 13C determination.
Normal statistical and systematic errors are 0.25 %. The total error will
be : [0.25^2 + 0.25^2]^0.5 = 0.356 %.
Note : It seems a little strange, that in the W & W method,
the LARGER the errors, the BETTER the CHI^2 test will become.
Formula W & W :
Consider a number of measurements -+errors : A-+a........N-+n
Mean X = [A/a^2 + ... + N/n^2]/[1/a^2 + .... + 1/n^2]
Variance: 1/(1/a^2 + ... + 1/n^2)
Error x = [1/(1/a^2 + ...1/n^2)]^0.5
Chi^2 = (A-X)^2/a^2 + ....(N-x)^2/n^2
Calculations :
Arizona :
| 701/33^2 + 690/35^2 + 606/41^2 + 591/30^2 |
2.2241414
|
| -------------------------------------------------- | = --------------- = 646 |
|
1/33^2 + 1/35^2 + 1/41^2 + 1/30^2
|
0.0034404
|
|
Error = [1/0.0034404]^0.5 = 290.7^2 = 17.05 = 17
|
Oxford :
| 795/65^2 + 745/55^2 + 730/30^2 |
0.7949403
|
| --------------------------------------- | = ------------- = 749 |
|
1/65^2 + 1/55^2 + 1/45^2
|
0.0010609
|
Zurich :
| 733/61^2 + 722/56^2 + 679/51^2 + 639/45^2 + 635^2 | 1.1992731 |
| ------------------------------------------------------------- | = ---------- = 676 |
|
1/61^2 + 1/56^2 + 1.51^2 + 1/45^2 + 1.57^2
|
0.0017734 |
Weighted Mean :
| 646/17^2 + 749/31^2 + 676/24^2 | 4.1883016 |
| -------------------------------------- | = ----------- = 671.55 = 672 |
|
1/17^2 + 1/31^2 + 1/24^2
|
0.0062368 |
Note : If we assume, as noted in Nature, that all dates have the same weight, then we can avoid rounding off and calculate the mean -+error as follows :
| 2.2241414 + 0.7949403 + 1.1992731 | 4.2183548 |
| ----------------------------------------- | = ------------- = 672 |
| 0.0034404 + 0.0010609 + 0.0017734 | 0.0062747 |
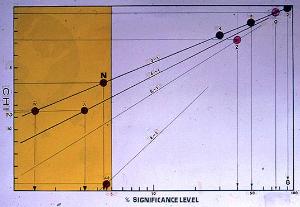
X^2 test:
Maximum 5.99 for 95% confidence and (3-1) degrees of freedom.
[(646-672)^2/17^2]+[(749-672)^2/31^2]+(676-672)^2/24^2] = 8.43
The computer, with NO ROUNDING OFF of the values, will give
X^2 = 8.76
|
|
Conclusion :
An X^2 test value 8.43 > 5.99 states that there is a
SIGNIFICANT
DIFFERENCE
between the results of the 3 laboratories. From the X^2
test result, one can determinate the % significance level : 2.718^-(8.43/2)
= 1.3 %. From this test, one may conclude, that the probability of obtaining,
by chance alone, a scatter as high as that observed for the Shroud, is
only 13 in 1000. Because we assume all radiocarbon dates to be correct,
we must conclude, that the SMALL samples, taken at the same place,
do not have the same radioactivity and are not REPRESENTATIVE for
the Shroud.
| Arizona | Oxford | Zurich | Mean | Chi^2 | S.L.% | |
| Nature | 646-+31 | 750-+30 | 676-+24 | 689-+16 |
6.4
|
5
|
| Computer | 646-+17 | 749-+31 | 676-+24 | 672-+13 |
8.4
|
1.3
|
Following the Nature report :
The spread of measurements for sample 1 (Shroud) is somewhat greater
than would be expected from the errors quoted. The X^2 test shows that
it is UNLIKELY, that the quoted errors FULLY reflect the
overall scatter. Not noted is, that a Chi^2 test value > 5.99 DOES EXCLUDE
the claimed 95 % confidence. In such cases, one should verify and reject
possible "outliers." Possible "outliers" are the Arizona dates 591 and
606, and the Oxford date 795. One may wonder why, the British Museum, did
not use the X^2 test for each laboratory.
X^2 test for Arizona (For 4-1 degrees of freedom X^2 = < 7.81)
| (701-646)^2 | (690-646)^2 | (646-606)^2 | (646-591)^2 | |
| -------------- | + ------------- | + ------------ | + ---------- | = 8.33 > 7.81 |
|
33^2
|
35^2
|
41^2
|
30^2
|
X^2 test for Oxford (For 3-1 degrees of freedom X^2 = <5.99)
| (795-749)2 | (749-745)^2 | (749-730)^2 | |
| ------------- | + --------------- | + ------------- | = 0.68 < 5.99 |
|
65^2
|
55^2
|
45^2
|
X^2 test for Zurich (For 5-1 degrees of freedom X^2. = <9.49)
| (733-676)^2 | (722-676)^2 | (679-676)^2 | (676-638)^2 | (676-635)^2 | |
| -------------- | + ------------ | + ------------ | + ------------ | + -------------- | = 2.69 |
|
61^2
|
56^2
|
51^2
|
45^2
|
57^2
|
X^2 for the Mean (For 3-1 degrees of freedom X^2 = <5.99)
| (749-672)^2 | (676-672)^2 | (672-646)^2 | |
| -------------- | + ------------- | + ------------- | = 8.54 > 5.99 |
|
31^2
|
24^2
|
17^2
|
The X^2 test indicates INCONSISTENCY for Arizona and the Mean.
But the British Museum, on finding "INCONSISTENCY" decided NOT
to check for outliers, but to BIAS the results for Arizona by enlarging
the error from 17 to 31. This shifts the UNBIASED mean date 672-+13
to 689-+16 and consequently the Chi^2 test value from 8.54 to 6.4 and also
the % significance level from 1.3 to 4.4. Finally, it was decided to REPLACE
the weighted mean 689-+16 by the UNWEIGHTED mean 691-+31 and to
ENLARGE the multiplying factor 1.96 to 2.6, based on an analysis
of variance on the 12 individual measurements. The number of degrees of
freedom (d), lying between (3-1) inter- and (12-3) intra- laboratory degrees
of freedom was ESTIMATED at 5.
Analysis of variance :
| Arizona | (701+690+606+591)/4 = 647 |
| Var. | (701-647)^2+(690-647)^2+(647-606)^2+(647-591)^2 = 9582 |
| Oxford | (795+745+730)/3 = 757 |
| Var. | (795-757)^2+(757-745)^2+(757-730)^2 = 2317 |
| Zurich | (733+722+679+639+635)/5 = 682 |
| Var. | (733-682)62+(722-682)^2+(682-679)^2+(682-639)^2+ (682-635)^2 = 8261 |
|
[9582/4 + 2317/3 + 8261/5]^2
|
| ------------------------------------------------------------------ = |
| ((9582/4)^2)/(4+1) + ((2317/3)^2)/(3+1) + ((8261/5)^2)/(5+1) |
| (2395.5 + 722.3 + 1652.2)^2 | 22752900 | |
| -------------------------------------- | = ------------ | = 13.13 = 13-3 = 10 |
| 1147684 + 130429.3 + 454960.8 | 1733074 |
The multiplying factor for d=10 and 97.5% confidence = 2.23. (This is for a two tail test and 1 -(2x0,25) = 95 % confidence). An analysis of variance based on 3 laboratories and 16 measurements will only differ for Arizona :
36587/8 = 4573.4 and 4573.4^2/9 = 2323973.1
|
[4573.4 + 722.3 + 1652.2]^2
|
48273314
|
|
| -------------------------------------- = | ------------ | = 16.59 = 17-3 = 14 |
| 2323973.1 + 130429.3 + 454960.8 |
2909363
|
Multiplying the factor for d=14 and 97.5 % confidence = 2.15.
Note : Following the Wilson & Ward method the variance is the squared quoted error.
Strictly following W & W :
|
[17^2/4 + 30^2/3 + 24^2/5]^2
|
|
| ------------------------------------------------------ | = 9.22 -3 = 6 |
| [(17^2/4)^2]/5 + [(30^2/3)^2]/4 + [(24^2/5)^2]/6 |
With Arizona error 31 :
|
[31^2/4 + 30^2/3 + 24^2/5]^2
|
|
| ----------------------------------------------------- | = 11.85 - 3 = 9 |
| [(31^2/4)^2]/5 + [(30^2/3)^2]/4 + [(24^2/5)^2]/6 |
These small differences may seem of little importance, but it is one more indication of a "biased" assessment, with the only purpose of a systematic enlargement of the error range. The same goes for the estimation of the error for the Shroud from the scatter. Here one "forgets" that quoted errors in AMS are deviated from NBS standards and blanks, measured during the SAME run with a series of targets, from the Shroud. Note that for samples 2, 3 and 4, the limits were obtained in the usual way.
This can be illustrated by the Chi^2 and the significance level, given
in table 2 (Nature).
| Sample |
1
|
2
|
3
|
4
|
| X^2 (2 d.f.) | 6.4 | 0.1 | 1.2 | 2.4 |
| Sig.Level % | 5 |
90 | 50 | 30 |
COMMENT :
The advice of Prof. Hoel (University of California) is : "In the case
of a X^2 test value close to the limit, it is better not to use such dates
in further calculations, but to ask for more and better dates." Despite
the use of the NBS standard (Oxalic Acid Standard SRM 4990) the results
for the radiocarbon dating of the Shroud show a SYSTEMATIC BIAS
and UNEXPLAINED VARIABILITY. An indication of the inhomogeneity
of the micro-samples, used in AMS.
Note : Theoretically, all statistical assessments should have been made BEFORE the dC13 correction to -25 o/oo has been applied. In this case the RAW Oxford date would have been -+ 40 years OLDER.
RAW RESULTS.
| Mean : | (646/17^2 ) + (790/31^2) + (676/24^2) | |
| ----------------------------------------- | = 678 -+ 13 | |
|
1/17^2 +1/31^2 + 1/24^2
|
| Chi^2 : |
(646-678)^2
|
(790-678)^2
|
(676-678)^2
|
|
| --------------- | + -------------- | + -------------- | = 17.49 > 5.99 | |
|
17^2
|
30^2
|
24^2
|
Their can be no doubt, the RAW Oxford results are probably "OUTLIERS." Let us say, that Oxford was saved by the dC13 determination, made IN ANOTHER laboratory.
CONCLUSION :
Facts :
The Arizona error was arbitrary enlarged from 17 to 31. The Wilson
& Ward mean 689-+16 was replaced by the UNWEIGHTED mean 691-+31.
The multiplying t-factor for 95% confidence was enlarged from 1.96 to 2.6.
The claimed "at least 95 % confidence" for the medieval dating of the Shroud
is NOT supported by statistical analysis. One may wonder, why these
OBVIOUS facts, were not spotted by the "team of peers" who judge
all papers before publication in Nature. Even stranger is the FACT,
that Prof. Bray of the "Istuto di Metrologia" of Turin, confirmed that
the results of the 3 labs were mutually compatible, and that, on the evidence
submitted, none of the means WERE questionable. Prof. Bray declared
not to be at liberty to answer any questions. His answer was : "On the
evidence submitted, no averaged results APPEAR questionable. The
scatter for sample 1 is about equal to the limit." The only possible explanation
is, that NOT all evidence was submitted to Prof. Bray. Prof. Bray
refused to comment on the "combination from EIGHT to FOUR
Arizona dates. I asked the editor of Nature, to compare my calculations
with the results given by Damon et al. Following Dr. Laura Garwin (Physical
Science Editor) : "You are asking me questions that are beyond my ability
to answer. The Damon et al paper was refereed by qualified referees and
no dissatisfaction was raised with the assignment or errors." I also asked
the advice of Prof. Bene (University of Geneve). "I would like to congratulate
you for the quality of your work. You established definitive evidence,
that the measurements made on the linen of the Shroud are NOT homogeneous
and that they should be rejected." Prof. Jouvenoux (University of Marseille-Aix)
: "Van Haelst was probably the first to question the radiocarbon dating
of the Shroud in a scientific way."
Note :
These calculations have been verified by : Dr. Leese (British Museum).
She argues that the differences are caused by the use of different weighting
systems! The French professional statisticians Bouclier de Carbon and Forestier,
agreed with my results. Dr. Hedges (Oxford) replied : "I do not need statistics....."
Dr. Woeffli (Zurich) and Dr. Damon (Arizona) did not reply.
Prof. Evin (Lyon. France) : "Statistics will not change the facts...."
This paper has been presented at the CIELT International Shroud Symposium.
Rome 1993. (Actes CIELT Rome. ISBN 2.868.39.311X Ed. Fr.X. Guibert Paris.
pages 207-218).
A REQUEST.
Please use your computer to verify the calculations made in this paper.
The W & W method is easily to program on a Lotus Spreadsheet. Let your
computer judge the Nature dates and this paper.
|
A
|
B
|
C
|
D
|
E
|
|
|
Age
|
Error
|
(b-)^2
|
(a-)/(c-)
|
1/(c-)
|
|
| 1 |
701
|
33
|
1089 | 701/1089=0.6437098 | 1/1089=0.0009182 |
| 2 |
690
|
35
|
1225 | 690/1225=0.5632653 | 1/1225=0.0008153 |
| 3 |
606
|
41
|
1681 | 606/1681=0.3604997 | 1/1681=0.0005948 |
| 4 |
591
|
30
|
900 | 591/ 900=0.6566666 | 1/ 900=0.0011111 |
| 5 | (d5)/(e5) | [1/(e5)]^0.5 | @sum = 2.2241414 | @sum = 0.0034394 |
a5 = Age = 2.2241414/0.0034294 = 646,6 = 647
b5 = Error = [1/0.0034394]^0.5 = 290.7^0.5 = 17.05 = 17
Repeat this for Oxford, Zurich and calculate the Weighted Mean-+Error
from the sub-means-+errors.
| The Chi^2 (X^2) test : | Example : |
| (Ar.Mean-W.Mean)^2/Ar.Error^2 | (646-672)^2/17^2 = 2.5130111 |
| (Ox.Mean-W.Mean)^2/Ox.Error^2 | (749-672)^2/31^2 = 6.1696149 |
| (Zu.Mean-W.Mean)^2/Zu.Error^2 | (676-672)^2/24^2 = 0.0277777 |
| Chi^2 = 8.7104037 |
APPENDIX.
HOW TO BIAS THE COMPUTER RESULTS, TOWARDS 691-+31 ?
The computer results differ TWO times SIGNIFICANTLY from
the Nature dates (Table 2).
| Arizona | Mean* | Mean$ | |
| Computer | 646-+17 | 672-+13 | 689-+16 |
| Nature | 646-+31 | 689-+16 | 691-+31 |
| Factor | 31/17 |
31/16 |
ESTIMATION OF INDIVIDUAL ERRORS (Table 1) IN FUNCTION OF 691-+31.
First the individual Arizona errors should be multiplied by a factor
of 31/17.
Secondly, all individual errors should be multiplied by a factor of
31/16.
Arizona |
x 31/17 |
x 31/16 |
Oxford |
x 31/16 |
Zurich |
x 31/16 |
701-+33 |
60
|
117
|
795-+65 |
126
|
733-+61 |
118
|
690-+35 |
64
|
124
|
745-+55 |
107
|
722-+56 |
108
|
606-+41 |
75
|
145
|
730-+45 |
87
|
679-+51 |
99
|
591-+30 |
55
|
106
|
639-+45 |
87
|
||
635-+57 |
110
|
Table 2 Errors on the mean.
Arizona error :
[1/(1/117^2 + 1/124^2 + 1/145^2 + 1/106^2)]^0.5 = 60
Oxford error :
[1/(1/126^2 + 1/107^2 + 1/87^2)]^0.5 = 60
Zurich error :
[1/(1/118^2 + 1/108^2 + 1/99^2 + 1/87^2 + 1/110)]^0.5 = 46
Mean age :
| 646/60^2 + 750/60^2 + 676/46^2 |
0.7072483
|
|
| ------------------------------------- | = -------------- | = 688 |
|
1/60^2 + 1/60^2 1/46^2
|
0.0012080
|
Error : [1/(1/60^2 + 1/60^2 + 1/46^2)]^0.5 = 31
X^2 test :
(689-646)^2/60^2 + (750-689)^2/60^2 + (689-676)^2/46^2 = 1.64
Significance level = 2.718^-(1.64/2) = 44 %
Comparison with X^2 and % Sig.Level.
C = Computer strictly W & W for sample 1.
CC = Computer with errors in function of final error 31.
| Sample |
C
|
1
|
4
|
CC |
3
|
2
|
| X^2 | 1.6 | 6.4 | 2.4 | 1.64 | 1.3 | 0.1 |
| S.L.% | 1.3 |
5
|
30 | 44 | 50 | 90 |
Conclusion : The computer estimated individual errors for the
Shroud, in function of error 31 on the unweighted mean 691 are NOT
abnormally high and NOT out of range for the claimed AMS accuracy.
A NEW STATISTICAL ASSESSMENT FOR AMS. RADIOCARBON DATES.
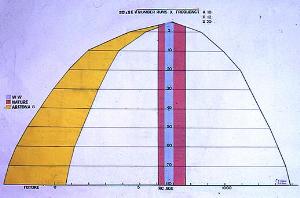
Because AMS radiocarbon dating results are NOT absolute values, but the result of a number of X runs, with a frequency Y, all results are given with a certain error. The more measurements closer to the UNKNOWN true value and TRUE error, the closer the averaged and error mean will become. Theoretically, an INFINITE number of measurements will yield a result INFINITELY close to the TRUE value-+ error. Practically, one has to take into account, the precision of the measurement and the systematic errors of the method.
Example : All Oxford sub-errors, lower than 40 have been rounded up to 40.
Following the Nature report, the radiocarbon age of the Shroud,
with a 95 % confidence, is 691-+31 years BP. (Before Present = 1950). By
backward calculation from this result, the INDIVIDUAL errors can
be estimated.
| Arizona | x 1.82 | 591-+ 55 | 701-+ 60 | 690-+ 64 | 606-+ 75 | ||
| All errors | x 1.94 | 591-+107 | 701-+116 | 690-+124 | 606-+145 | (Ar) | |
| 795-+126 | 745-+107 | 730-+ 87 | (Ox) | ||||
| 733-+118 | 722-+108 | 679-+ 99 | 639-+ 87 | 635-+110 | (Zu) |
Because THEORETICALLY, any measurement between the limits
606 - 145 = 416 and 795 + 126 = 921
can be the TRUE date, a
good estimation of the 95% confidence range can obtained from a
DOUBLE
statistical analysis based on MINIMUM and MAXIMUM values.
|
Minimum
|
Maximum
|
||||||
Ari. |
Oxf. |
Zur. |
Ari. |
Oxf. |
Zur. |
||
484 |
669 |
615 |
698 |
921 |
851 |
||
585 |
638 |
614 |
817 |
852 |
830 |
||
566 |
643 |
580 |
814 |
817 |
778 |
||
461 |
552 |
751 |
726 |
||||
525 |
745 |
||||||
Tot. |
2096 |
1950 |
2887 |
3072 |
2590 |
3930 |
|
Mean |
524 |
650 |
577 |
768 |
863 |
786 |
|
Er. |
33 |
10 |
18 |
28 |
31 |
29 |
|
W.Mean. |
578
|
799
|
|||||
Error |
37
|
30
|
|||||
95 % |
578-(2x37)=504 |
799+(2x30)=859 |
|||||
Any date between those limits 504-859 can be the TRUE date. Here,
about 30 % of this age range will be YOUNGER than the HISTORICAL
age of 1355 AD.
The Bienayme-Tchebychev formula.
In the case of non normal distributed dates, the error multiplying
factors can be estimated, by the Bienayme-Tchebychec inequality.
Probability : {[X-M] < MF X SIGMA} > 1-1/MF^2.
Thus MF for:
68 % = 1-1/1.77^2 = 1-1/3.31 = 1-0.32 = 0.68
75 % = 1-1/2.00^2 = 1-1/4.00 = 1-0.25 = 0.75
90 % = 1-1/3.16^2 = 1-1/10.0 = 1-0.10 = 0.90
95 % = 1-1/4.47^2 = 1-1/20.0 = 1-0.05 = 0.95
The error range for 691-+31 at 95% confidence will be :
691-(4.47x31) = 552 < 691 < 830 = 691+(4.47X31)
Here about 21 % of this age range will be YOUNGER than the HISTORICAL age of 1355 AD. It is clear, that such large errors are unacceptable for the precision claimed for AMS age rc. determinations. (Source Prof. Jouvenoux. University of Marseille-Aix. France).